LeetCode Weekly Contest 22（双周赛）

算法

字数统计: 1.7k阅读时长: 7 min

 2020/03/22   Share

总的来说题目挺简单的。晚上做题注意力没那么集中，看错几次题，浪费不少时间，可惜了。

两个数组间的距离值

题目描述

给你两个整数数组 arr1 ， arr2 和一个整数 d ，请你返回两个数组之间的距离值。

距离值定义为符合此描述的元素数目：对于元素 arr1[i] ，不存在任何元素 arr2[j] 满足 |arr1[i]-arr2[j]| <= d 。

解法

两重循环遍历一下就行。

func findTheDistanceValue(arr1 []int, arr2 []int, d int) int {
    ans := 0
    for i := range arr1 {
        flag := true
        for j := range arr2 {
            if abs(arr1[i]-arr2[j]) <= d {
                flag = false
                break
            }
        }
        if flag {
            ans++
        }
    }
   	return ans
}

func abs(x int) int {
    if x > 0 {
        return x
    }
    return -x
}

安排电影院座位

题目描述

如上图所示，电影院的观影厅中有 n 行座位，行编号从 1 到 n ，且每一行内总共有 10 个座位，列编号从 1 到 10

给你数组 reservedSeats，包含所有已经被预约了的座位。比如说，researvedSeats[i] = [3,8] ，它表示第 3 行第 8 个座位被预约了。

请你返回最多能安排多少个 4 人家庭。4 人家庭要占据同一行内连续的 4 个座位。隔着过道的座位（比方说 [3,3] 和 [3,4]）不是连续的座位，但是如果你可以将 4 人家庭拆成过道两边各坐 2 人，这样子是允许的。

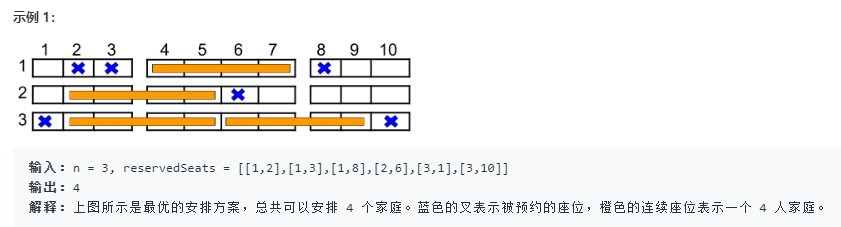
提示：

1 <= n <= 10^9
1 <= reservedSeats.length <= min(10*n, 10^4)
reservedSeats[i].length == 2
1 <= reservedSeats[i][0] <= n
1 <= reservedSeats[i][1] <= 10
所有 reservedSeats[i] 都是互不相同的。

解法

由于限制了跨过道的坐法只能有一种，即每边坐两人，所以每一排座位的坐法就只有 4 种情况。

4、5、6、7
2、3、4、5
6、7、8、9
2、3、4、5 和 6、7、8、9

题目求的是最多能安排多少个家庭座位，所以第四种优先安排。

剩下的难点在于数据量比较大，如果直接遍历 n 是会超时的。

注意到 reservedSeats.length <= min(10*n, 10^4)，范围比较小，就从这下手。

func maxNumberOfFamilies(n int, reservedSeats [][]int) int {
    m := make(map[int][]bool)
    for _, reservedSeat := range reservedSeats {
        if len(m[reservedSeat[0]]) == 0 {
            m[reservedSeat[0]] = make([]bool, 11)
        }
        m[reservedSeat[0]][reservedSeat[1]] = true
    }
    ans := 0
    for _, isSeat := range m {  // 只关注有座位被占用的部分，整排为空的一定能坐下两家庭
        if isSeat[2] || isSeat[3] || isSeat[8] || isSeat[9] {
            if !isSeat[4] && !isSeat[5] && !isSeat[6] && !isSeat[7] {
                ans++
                continue
            }
        }
        if !isSeat[2] && !isSeat[3] && !isSeat[4] && !isSeat[5] {
            ans++
        }
        if !isSeat[6] && !isSeat[7] && !isSeat[8] && !isSeat[9] {
            ans++
        }
    }
    return 2*(n-len(m)) + ans  // 空座位一定能坐下两个家庭
}

还有一种思路，每个座位只有被占用 / 空两种状态，很容易想到用位运算处理。

将整数按权重排序

题目描述

我们将整数 x 的权重定义为按照下述规则将 x 变成 1 所需要的步数：

如果 x 是偶数，那么 x = x / 2
如果 x 是奇数，那么 x = 3 * x + 1

比方说，x=3 的权重为 7 。因为 3 需要 7 步变成 1 （3 –> 10 –> 5 –> 16 –> 8 –> 4 –> 2 –> 1）。

给你三个整数 lo， hi 和 k 。你的任务是将区间 [lo, hi] 之间的整数按照它们的权重升序排序，如果大于等于 2 个整数有相同的权重，那么按照数字自身的数值升序排序。

请你返回区间 [lo, hi] 之间的整数按权重排序后的第 k 个数。

注意，题目保证对于任意整数 x （lo <= x <= hi），它变成 1 所需要的步数是一个 32 位有符号整数。

提示：

1 <= lo <= hi <= 1000
1 <= k <= hi - lo + 1

解法

一开始纠结了一会求权重，后面发现直接模拟就好了，并不是每次决策，求最小步数。

func getKth(lo, hi, k int) int {
    power := make(map[int]int)
    arr := make([]int, hi-lo+1)
    for i := lo; i <= hi; i++ {
        arr[i-lo] = i
        getPower(i, power)
    }

    // 到这里就变成了常规 Top K 问题，简单做下排序吧，注意要稳定排序
    sort.Slice(arr, func(i, j int) bool {
        if power[arr[i]] != power[arr[j]] {
            return power[arr[i]] < power[arr[j]]
        }
        return arr[i] < arr[j] // 相等的留在原地
    })

    return arr[k-1]
}

func getPower(x int, power map[int]int) int {
    ans, tmp := 0, x
    for x != 1 {
        if x&1 == 1 {
            x = 3*x + 1
        } else {
            x /= 2
        }
        ans++
        if val, ok := power[x]; ok {
            ans += val
            break
        }
    }
    power[tmp] = ans
    return ans
}

3n 块披萨

题目描述

给你一个披萨，它由 3n 块不同大小的部分组成，现在你和你的朋友们需要按照如下规则来分披萨：

你挑选任意一块披萨。

Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。

Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。

重复上述过程直到没有披萨剩下。

每一块披萨的大小按顺时针方向由循环数组 slices 表示。

请你返回你可以获得的披萨大小总和的最大值。

示例 1：

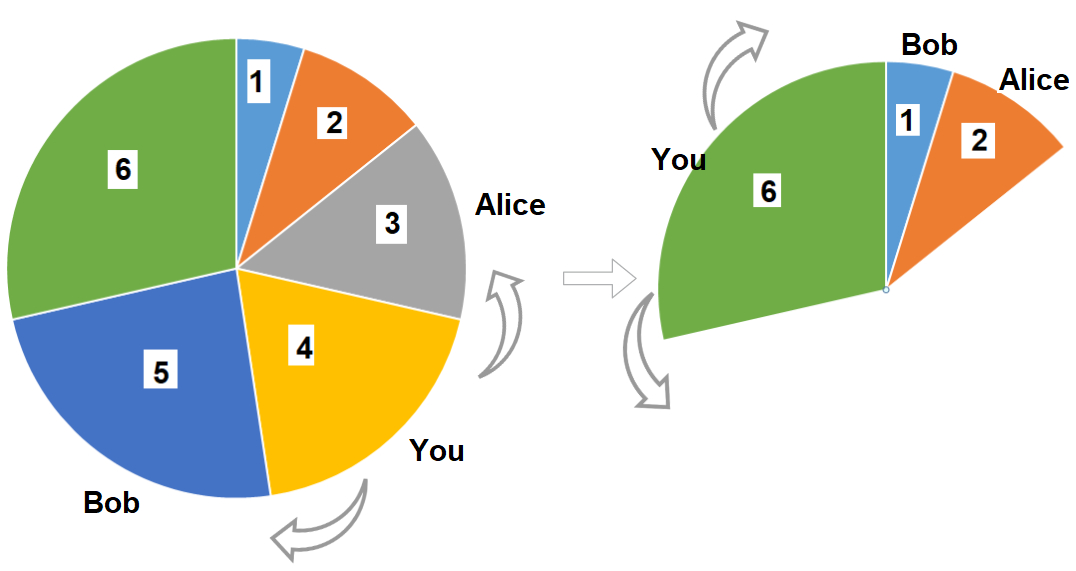
输入：slices = [1,2,3,4,5,6]
输出：10
解释：选择大小为 4 的披萨，Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨，Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。

示例 2：

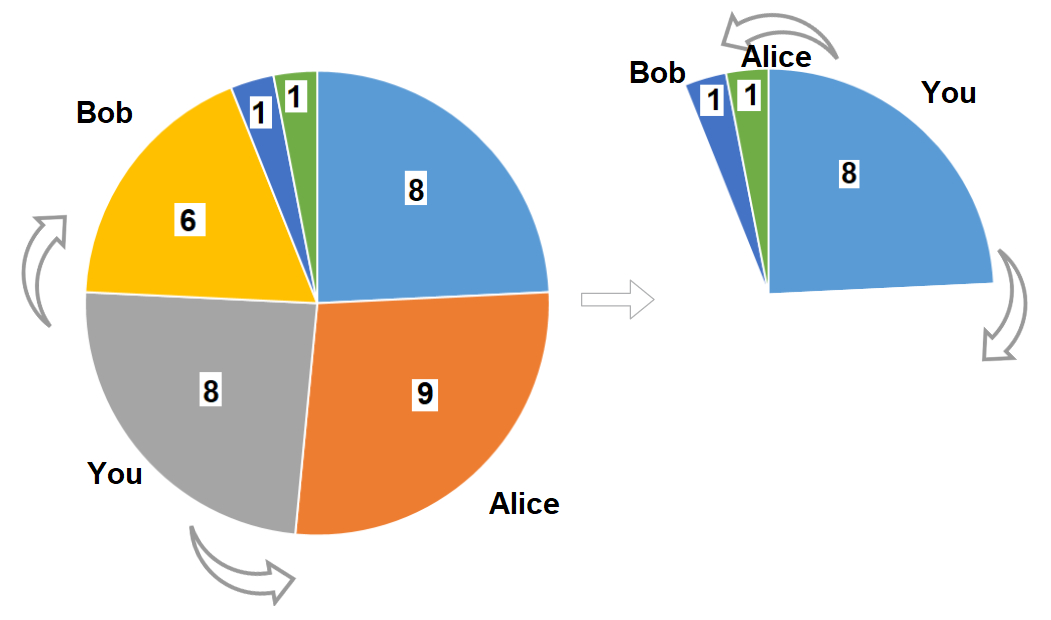
输入：slices = [8,9,8,6,1,1]
输出：16
解释：两轮都选大小为 8 的披萨。如果你选择大小为 9 的披萨，你的朋友们就会选择大小为 8 的披萨，这种情况下你的总和不是最大的。

示例 3：

输入：slices = [4,1,2,5,8,3,1,9,7]
输出：21

示例 4：

输入：slices = [3,1,2]
输出：3

提示：

1 <= slices.length <= 500
slices.length % 3 == 0
1 <= slices[i] <= 1000

解法

这题直接贪心显然不行，两个特点，一个是形成环，并且选了这个，其左右两边的将被丢弃。

很容易联想到类似的题，即打家劫舍系列里的不能偷相邻的，以及房子围成圆形。

所以问题就转化为——不相邻有限子数列的最大和，该子数列不能同时包含首尾。

即在大小为 3n 的数组中挑选 n 个满足上面条件的数。比如 1~9 披萨时的情况，只能拿走三份。

  idx 1 2 3 4 5 6 7 8 9
case1 -   -   -
case2 -   -       -
case3 -     -   -
case4   -     -   -

// TODO 代码还有点小问题，需要调调

原文作者：wywwzjj

原文链接：https://wywwzjj.top/2020/03/22/LeetCode-Weekly-Contest-22/

发表日期：March 22nd 2020, 12:18:38 am

更新日期：May 15th 2021, 11:53:20 am

Next Post

LeetCode Weekly Contest 181
Previous Post

LeetCode 数据库专题

CATALOG

1. 两个数组间的距离值
1. 1.1. 题目描述
2. 1.2. 解法
2. 安排电影院座位
1. 2.1. 题目描述
2. 2.2. 解法
3. 将整数按权重排序
1. 3.1. 题目描述
2. 3.2. 解法
4. 3n 块披萨
1. 4.1. 题目描述
2. 4.2. 解法

